ARC072E Alice in linear land < DP >

Problem

Alice in linear land

$\mathrm{Time\;limit:\;2\;Sec}$
$\mathrm{Memory\;limit:\;256\;MB}$

Statement

Alice lives on a line. Today, she will travel to some place in a mysterious vehicle. Initially, the distance between Alice and her destination is $D$. When she input a number $x$ to the vehicle, it will travel in the direction of the destination by a distance of $x$ if this move would shorten the distance between the vehicle and the destination, and it will stay at its position otherwise. Note that the vehicle may go past the destination when the distance between the vehicle and the destination is less than $x$.
Alice made a list of $N$ numbers. The $i^{th}$ number in this list is $d_i$. She will insert these numbers to the vehicle one by one.
However, a mischievous witch appeared. She is thinking of rewriting one number in the list so that Alice will not reach the destination after $N$ moves.
She has $Q$ plans to do this, as follows:
Rewrite only the $q_i^{th}$ number in the list with some integer so that Alice will not reach the destination.
Write a program to determine whether each plan is feasible.

Constraints

$1\le N\le5\times10^5$
$1\le Q\le5\times10^5$
$1\le D\le10^9$
$1\le d_i\le10^9\;(1\le i\le N)$
$1\le q_i\le N\;(1\le i\le Q)$
$D$ and each $d_i$ are integers.

Input

Input is given from Standard Input in the following format:
$N\;D$
$d_1\;d_2\;\cdots\;d_N$
$Q$
$q_1\;q_2\;\cdots\;q_Q$

Output

Print $Q$ lines. The $i^{th}$ line should contain YES if the $i^{th}$ plan is feasible, and NO otherwise.

Sample

Input #1

4 10
3 4 3 3
2
4 3

Output #1

NO

Explanation #1
For the first plan, Alice will already arrive at the destination by the first three moves, and therefore the answer is NO. For the second plan, rewriting the third number in the list with $5$ will prevent Alice from reaching the destination as shown in the following figure, and thus the answer is YES.

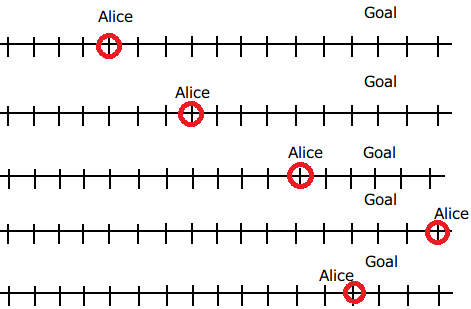
Input #2

5 9
4 4 2 3 2
5
1 4 2 3 5

Output #2

YES
YES
YES
YES
YES

Explanation #2
Alice will not reach the destination as it is, and therefore all the plans are feasible.
Input #3

6 15
4 3 5 4 2 1
6
1 2 3 4 5 6

Output #3

NO
NO
YES
NO
NO
YES

标签：DP

Translation

有一个无限长的数轴，你现在在$D$处，有$N$条指令，每条指令为一个整数$d_i$。顺次处理每条指令，如果你当前在$x$处，你会走到$\min(x,|x-d_i|)$处。有$Q$条询问，对于每条询问，回答能否通过改变$d_{q_i}$的值使得最后不能到达$0$。

Solution

精妙的做法，有点类似构造，又有点像$\mathrm{DP}$。

首先处理出数组$A$，其中$A_i$表示在没有更改指令的情况下，处理前$i$条指令后的位置。那么如果能够修改$d_i$，我们可以在处理完$d_i$后到达$[0,A_{i-1}]$中的所有位置。我们需要找到一个数组$B$，其中$B_i$表示修改并处理完$d_i$后，至少要在哪个位置才能使处理完后面的指令后不能到达$0$。显然，如果$A_{q-1}\ge B_q$，一定能找到可行方案，否则一定不能。

考虑如何得到$B$。我们倒序计算$B$。首先，显然有$B_n=1$。不难发现$B$一定是递减的，于是倒序计算时我们用前面的值作为基础值来处理出现在处理到的$B$。对于$B_i\;(i\in[1,n))$，$B_i$不小于$B_{i+1}$，如果$2B_{i+1}\le d_{i+1}$，那么从$B_{i+1}$位置进行$d_{i+1}$指令一定不会走到更小的点上，因此$B_i$可以取到其最小值$B_{i+1}$；否则，需要使其操作$d_{i+1}$后不小于$B_{i+1}$，因此$B_i=B_{i+1}+d_{i+1}$。

处理出$A,B$后判断即可。时间复杂度$O(N+Q)$。

Code

#include <bits/stdc++.h>
#define MAX_N 500000
using namespace std;
template <class T> inline void read(T &x) {
    x = 0; int c = getchar(), f = 1;
    for (; !isdigit(c); c = getchar()) if (c == 45) f = -1;
    for (; isdigit(c); c = getchar()) (x *= 10) += f*(c-'0');
}
int n, d[MAX_N+5], a[MAX_N+5], b[MAX_N+5];
int main() {
    read(n), read(a[0]), b[n] = 1;
    for (int i = 1; i <= n; i++) read(d[i]);
    for (int i = 1; i <= n; i++)
        a[i] = min(a[i-1], abs(a[i-1]-d[i]));
    for (int i = n-1; i; i--)
        if (b[i+1] <= d[i+1]/2) b[i] = b[i+1];
        else b[i] = b[i+1]+d[i+1];
    int m; read(m);
    while (m--) {
        int p; read(p);
        if (b[p] <= a[p-1]) puts("YES");
        else puts("NO");
    }
    return 0;
}