Problem
最大团
TimeLimit:10Sec
MemoryLimit:256MB
Description
给出平面上N个点的坐标,和一个半径为R的圆心在原点的圆。
对于两个点,它们之间有连边,当且仅当它们的连线与圆不相交。
求此图的最大团。
第一行两个整数N和R, 表示点数和圆的半径。
接下来N行,每行两个整数xi和yi,表示第i个点的坐标
保证每个点都严格在园外,且两两直线不与圆相切。
Output
输出一个整数:最大团的大小。
1
2
3
4
5
6
7
| 6 3
0 6
-7 -4
-3 -2
7 -5
-2 3
8 -3
|
Sample Output
HINT
对于100%的数据,1≤N≤2000,∣xi∣,∣yi∣,R≤5000
标签:DP
Solution
好题,非二分图的最大团是NP−Hard的,然而这道题有特殊性质。
从每个点向圆作切线,记下其覆盖的弧,过两个点的直线与圆相交当且仅当呈现下列两种情况:
-
两段弧相离
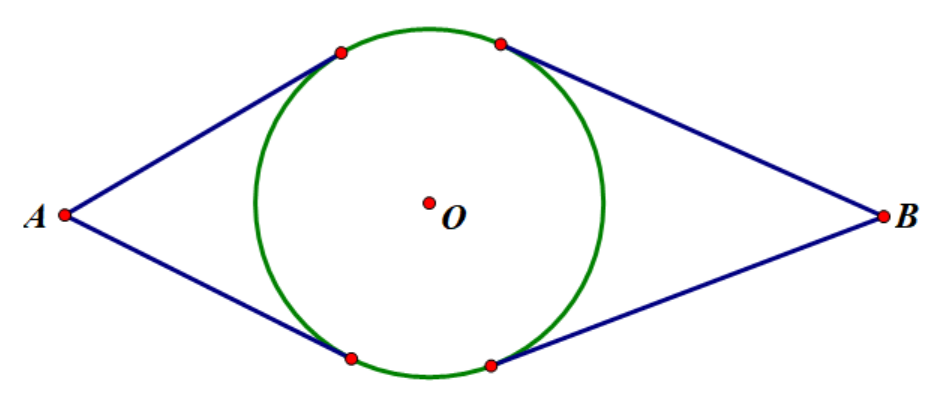
-
两段弧存在包含关系
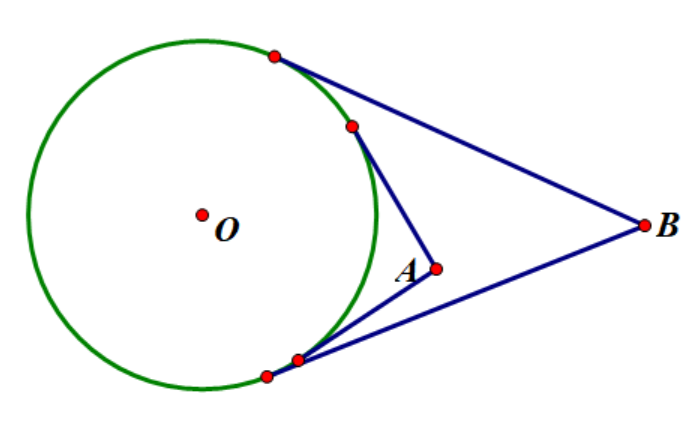
于是选出的所有点所对应的弧必须两两相交但不包含,于是设第i个点的弧的两端点为li,ri,最后的答案集合一定有
l1<l2<l3<⋯<lm<r1<r2<⋯<rm
将所有点按l值排序,则需要选出r的最长上升子序列,并且要满足lm<r1。
于是枚举每个点作为起点,向后DP,每次取最大值即可。
时间复杂度O(n2logn)
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <bits/stdc++.h>
#define MAX_N 2000
#define Pi acos(-1)
#define INF 0x3f3f3f3f
using namespace std;
typedef double dnt;
template <class T> inline void read(T &x) {
x = 0; int c = getchar(), f = 1;
for (; !isdigit(c); c = getchar()) if (c == 45) f = -1;
for (; isdigit(c); c = getchar()) (x *= 10) += f*(c-'0');
}
int n, m, mx; dnt r, p[MAX_N+5];
struct arc {dnt x, y;} s[MAX_N+5];
bool cmp(const arc &a, const arc &b) {
return a.x == b.x ? a.y < b.y : a.x < b.x;
}
int main() {
read(n), read(r);
for (int i = 1; i <= n; i++) {
dnt x, y; read(x), read(y);
if (x*x+y*y <= r*r) continue;
dnt ang1 = atan2(y, x);
dnt ang2 = acos(r/sqrt(x*x+y*y));
s[++m] = (arc){ang1-ang2, ang1+ang2};
if (s[i].x < -Pi) s[i].x += 2*Pi, swap(s[i].x, s[i].y);
if (s[i].y > Pi) s[i].y -= 2*Pi, swap(s[i].x, s[i].y);
}
n = m, sort(s+1, s+n+1, cmp);
for (int i = 1; i <= n; i++){
for (int j = 0; j < n; j++) p[j] = INF;
for (int j = i+1; j <= n && s[i].y > s[j].x; j++)
if (s[i].y < s[j].y) *lower_bound(p, p+n, s[j].y) = s[j].y;
mx = max(mx, (int)(lower_bound(p, p+n, INF)-p)+1);
}
return printf("%d\n", mx), 0;
}
|

